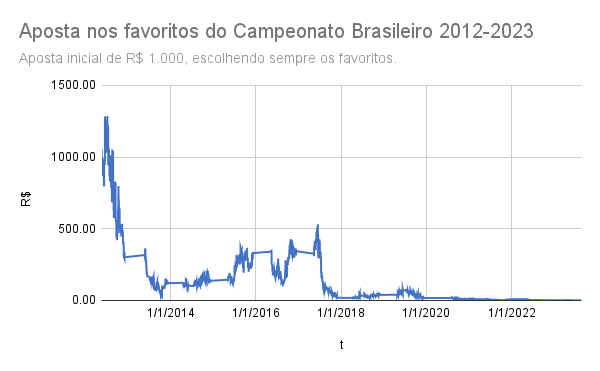
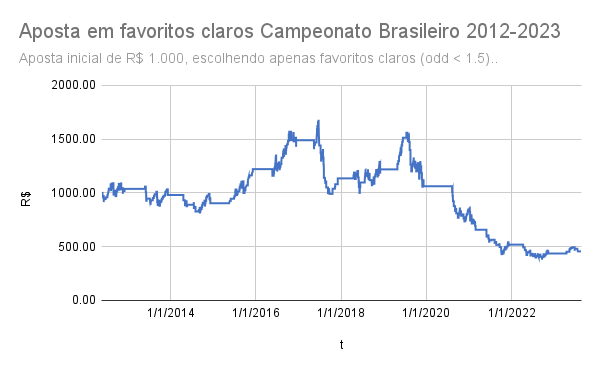
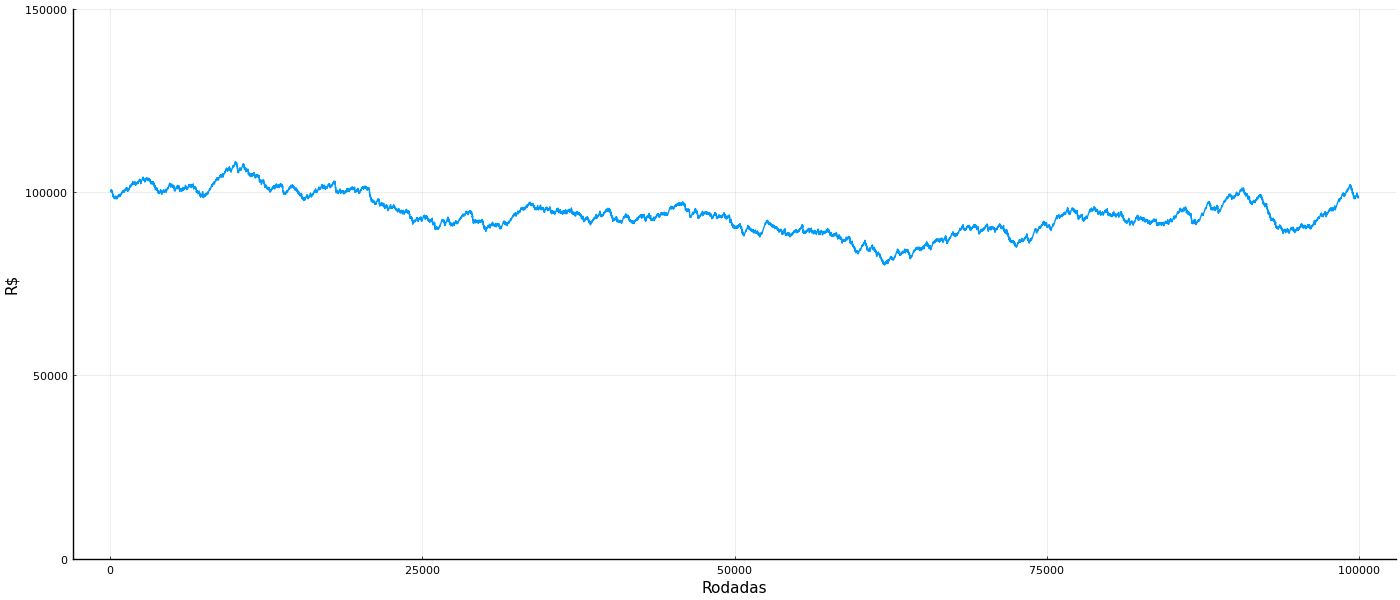
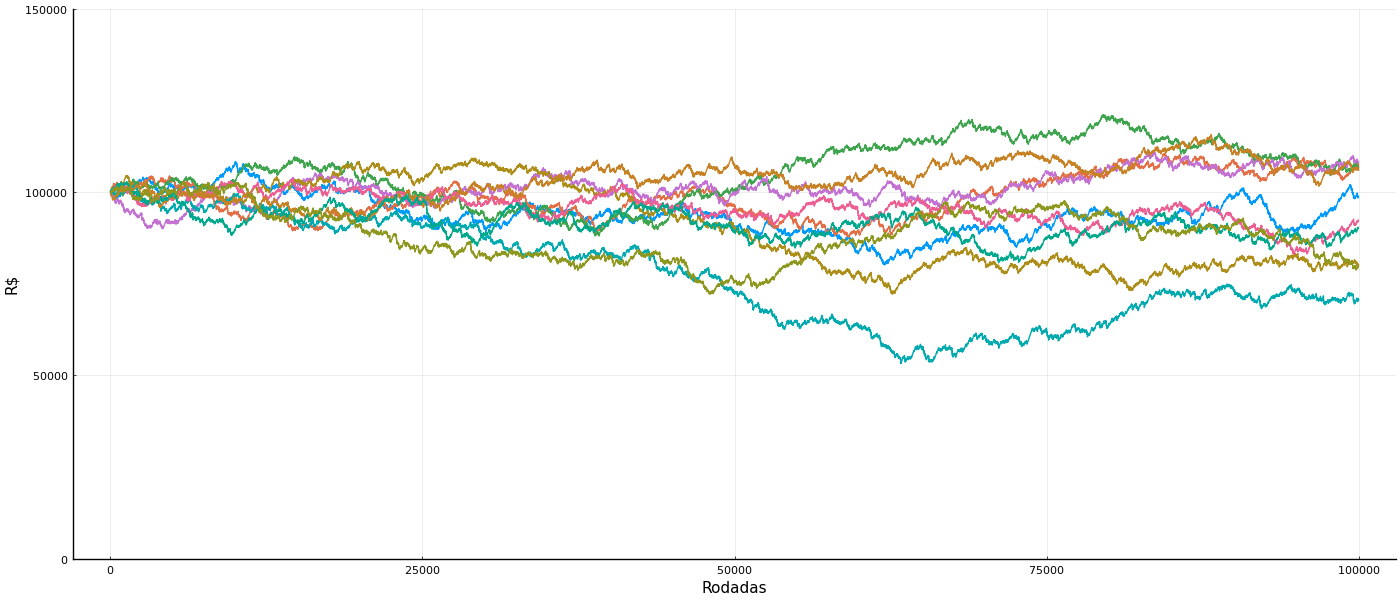
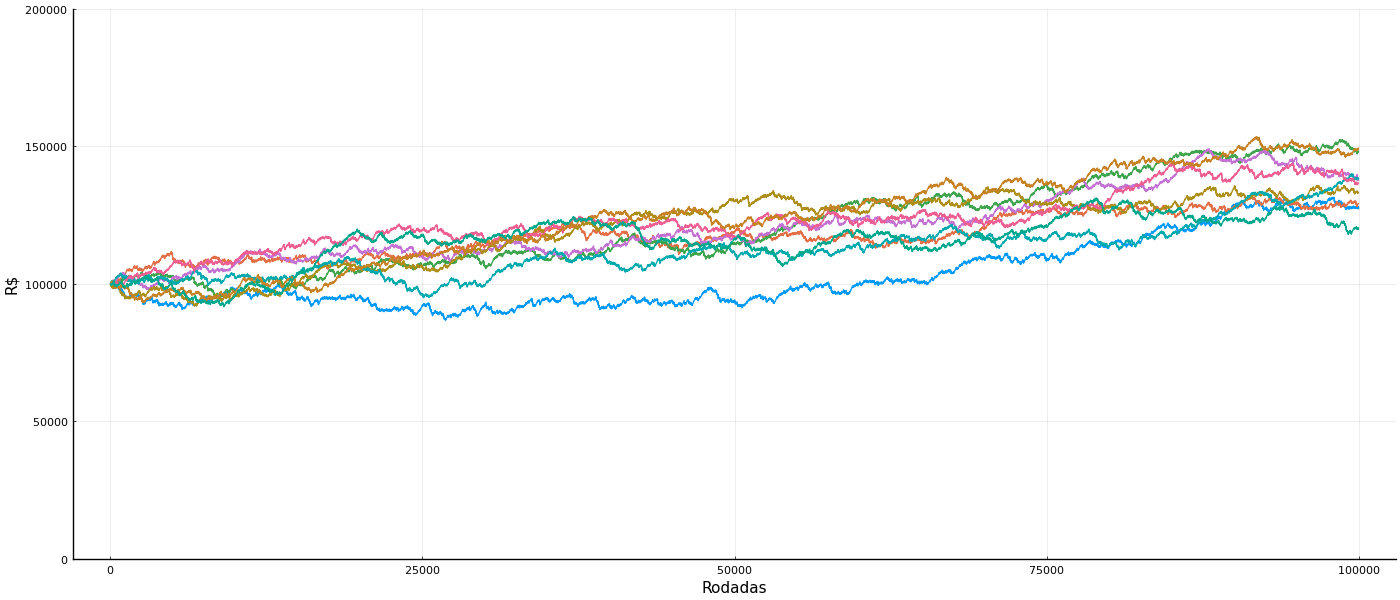
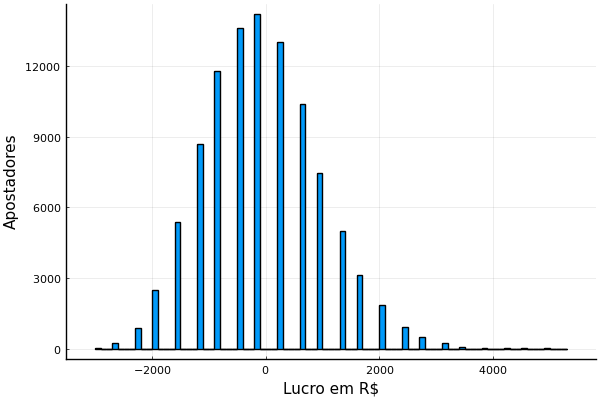
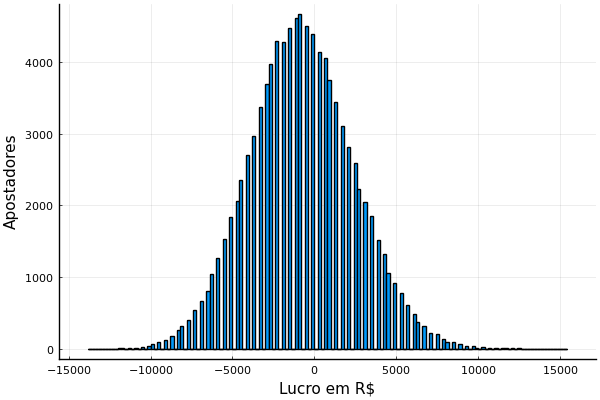
Atenção: apostas esportivas são feitas para você perder. O retorno esperado de apostas esportivas é perder dinheiro. Sites de apostas esportivas não são confiáveis: mesmo se você ganhar, pode perder o prêmio por fraude. O fato de eu escrever sobre o assunto não quer dizer que eu sou a favor. Não gaste dinheiro com apostas esportivas. Jamais ache que apostas esportivas são uma fonte de renda. Se você ler a série que vou escrever vai saber detalhes de como isso funciona, mas quero botar a conclusão já aqui em cima. Simplesmente. Não. Aposte.
Como funciona uma aposta esportiva
Uma aposta esportiva moderna, como a que se faz em todas as dezenas de sites de “bets” que se espalharam no Brasil, funciona sob o sistema de quota fixa: ao apostador é dada uma chance de apostar em um resultado, pelo qual ele receberá um retorno conhecido de antemão caso aquele resultado se concretize.
Estou olhando um site de apostas e vejo uma oferta de um jogo da série B que acontecerá em algumas horas. A oferta é:
Mandante: 1.909
X: 3.25
Visitante: 4.20
É possível apostar qualquer valor, e o número que é dado é o multiplicador do prêmio. Se eu apostar R$ 10 no mandante, e ele ganhar, vou receber:
$ 10 \times 1.909 = 19.09$
Caso eu erre a aposta (por empate, ou porque o time visitante venceu), perderei a totalidade do dinheiro.
A aposta no “X” é uma aposta no empate.
Sem nem conhecer que times estão envolvidos, já temos uma informação interessante: o time mandante é o favorito, porque o prêmio pago é menor caso ele ganhe. Caso a aposta seja no time visitante, o prêmio é consideravelmente maior:
$ 10 \times 4.20 = 42.00 $
Esses multiplicadores, chamados pelo termo inglês odds, são definidos pela empresa de apostas, e a definição dos odds é um grande segredo comercial e o sucesso da casa de apostas depende de escolher bem esses números.
Um detalhe importante: os números dos odds podem mudar com o tempo, à medida que apostas são feitas. De forma geral, se muita gente apostar em um time, os odds vão cair, enquanto os odds do outro time sobem. Mas uma vez feita a sua aposta, seus odds para aquela aposta são fixos. Isso quer dizer que apostadores que fizeram a aposta em momentos diferentes podem receber prêmios diferentes, mas o prêmio é conhecido no momento da aposta porque os odds de apostas feitas não mudam.
Também é permitido fazer várias apostas, mesmo no mesmo jogo. Por exemplo, um apostador aposta que o time mandante vai ganhar, aposta R$ 10 e recebe odds de 1.909 por isso. Digamos que antes da partida acontecer, sai a notícia de que um jogador importante do time visitante não vai participar: os odds do mandante vão mudar para um valor menor porque a possibilidade de vitória do time aumentou. O apostador, ainda mais confiante da vitória aposta mais 10 reais, mas dessa vez ganha um odd menos favorável de 1.3. No final, ele ganhará, em reais:
$ 10 \times 1.909 + 10 \times 1.3 = 32.09 $
Também não há impedimento algum contra apostar em resultados incoerentes: em uma vitória do mandante, e uma vitória do visitante, ao mesmo tempo. É comum apostadores fazerem isso quando fatos novos acontecem que mudam as expectativas de vitória de um ou outro time. Todas as apostas continuam válidas.
Algumas variantes
Torcedores não gostam de empates, e por isso as casas de apostas permitem outras variantes de apostas.
Por exemplo, existe a aposta de chance dupla. Para a mesma partida acima, a casa de apostas sugere:
1X: 1.222
12: 1.286
X2: 1.85
A aposta “1X” quer dizer “se o mandante (1) ganhar ou se o empate (X) acontecer”. “12” significa “se o mandante (1) ou o visitante (2) ganharem (não ouver empate)”. Obviamente “X2” quer dizer que o apostador ganha se acontecer empate ou vitória do visitante.
Mais uma variante é o empate sem aposta. Ainda para a mesma partida, temos as ofertas:
Mandante: 1.364
Visitante: 2.875
Nesse caso, a aposta é apenas sobre a vitória de um time ou outro – mas em caso de empate, o apostador recebe o dinheiro da aposta de volta. Note como os odds são diferentes (e obviamente menos favoráveis) do que no caso em que o empate é aceito.
Há muitas outras formas de apostas – saldo de gols, diferença de gols, resultado com handicap, resultados do primeiro ou do segundo tempo, etc. Há aposta sobre quais jogadores vão marcar gol, ou qual o primeiro jogador que vai marcar. Ou com quantos minutos de jogo vai acontecer o primeiro gol, ou quantas faltas, ou escanteios acontecerão. De forma geral, quanto mais exótico e específico o tipo de aposta, piores as chances do apostador ganhar algo, por motivos que explicaremos mais em frente.
Pensando em termos de probabilidades
Podemos pensar em uma partida como um processo aleatório: não há como saber, mesmo com toda informação disponível, quem vencerá uma partida.
Isso não quer dizer que as probabilidades de vencer a partida são bem distribuídas: um time muito mais forte tem mais chance de vencer sobre um time fraco, mas o time fraco pode vencer sobre o forte.
Na Copa de 2022, a seleção vencedora, a Argentina, perdeu para o time da Arábia Saudita por 2 a 1 no seu primeiro jogo na competição. A Argentina era, de maneira avassaladora, a favorita para vencer esse jogo. E no entanto a Argentina perdeu.
Uma maneira de representar essas diferenças é pensando em termos de probabilidades. Uma estimativa para o resultado dessa partida (e não importa muito como isso foi calculado, mas que parece plausível), dava as seguintes probabilidades antes do jogo:
Argentina: 85%
Empate: 12%
Arábia Saudita: 3%
Ao contrário do que se costuma achar, uma probabilidade maior da Argentina vencer não é uma previsão de que a Argentina vai vencer.
Uma maneira de interpretar esses números é assim: imagine que ao invés de haver um único jogo, nesse momento sejam jogadas 100 partidas simultâneas entre esses dois times em um multiverso. A previsão diz que na média, em 85 dessas partidas a Argentina venceria, em 12 partidas haveria um empate e em 3 partidas a Arábia Saudita venceria.
No mundo real, só temos uma partida. Quando a Arábia Saudita ganha, o resultado não está errado: por acaso, estamos vivendo em um dos multiversos em que a Arábia Saudita ganhou. Improvável, mas não impossível.
Pensando como a casa de apostas: interpretando os odds
Suponha que exista um site de apostas não comercial, que não tenha lucro como objetivo. Tudo que ele faz é receber apostas e redistribuir o dinheiro dos perdedores das apostas para os vencedores, de maneira justa, de forma que os apostadores corretos sejam recompensados e os apostadores errados sejam punidos.
Suponha que, através dos modelos matemáticas dessa casa de apostas, chegou-se à conclusão infalível de que o time mandante tem 50% de chances de vencer, e que há 25% de chances de empate, e 25% de chances de que o time visitante ganhe. Suponha também que os apostadores fazem apostas fixas de R$ 10 (para simplificar o exemplo) e que são pessoas bem informadas.
O conceito de apostador informado é importante para a análise: é um apostador virtual, com acesso a todas as informações necessárias, e faz apostas por motivos puramente financeiros. É o melhor apostador possível. O apostador informado não ganha sempre – mas na média ele ganha mais que qualquer outro apostador.
Um bom odd inicial seria:
Mandante: 2.0
Empate: 4.0
Visitante: 4.0
Apostadores, mesmo informados, nunca vão acertar todas as apostas, mas de forma geral a quantidade de apostas deles vai seguir uma distribuição parecida com a probabilidade real de vitória. Ou seja, é esperado que mais apostadores informados apostem no mandante nesse caso, e menos no empate ou visitante, na mesma proporção da probabilidade real.
Digamos que nessa casa de apostas não-lucrativa que tem apenas apostadores informados, nós coletemos 100 apostas. O esperado é que os apostadores informados, que podem apostar apenas R$ 10, apostem aproximadamente da seguinte forma:
Mandante: 50 apostas = R\$ 500
Empate: 25 apostas = R\$ 250
Visitante: 25 apostas = R\$ 250
Para um total de R$ 1000 apostados. Vamos ver o que acontece se cada resultado se concretizar:
Se o mandante vencer, cada apostador no mandante receberá, em reais:
$ 10 \times 2.0 = 20 $
Como são 50 apostadores, R$ 1000 serão distribuídos para os vencedores, o que é a totalidade do que foi apostado. Os demais apostadores perdem suas apostas.
Em caso de vitória do visitante, cada apostador no visitante receberá, em reais:
$ 10 \times 4.0 = 40$
Como são 25 apostadores, o total distribuído é novamente a totalidade de R$ 1000 (25 x 40 = 1000). Os perdedores levam zero, e a casa de apostas sem fim lucrativo recebe também zero. Um caso similar acontece se ocorrer empate.
As apostas e os prêmios estão balanceados. A casa de apostas não-lucrativa funciona bem!
De probabilidades para odds
No exemplo anterior, definimos que a vitória do mandante tinha 50% de chance de acontecer, e demos para os apostadores um odd de 2.0. Por quê? A relação entre odd e probabilidade é:
$ \text{odd} = \frac{1}{\text{probabilidade}} $
ou de maneira equivalente:
$ \text{probabilidade} = \frac{1}{\text{odd}} $
Lembrando também que é possível representar uma probabilidade de 100% como o número 1.0, uma probabilidade de 50% como 0.5, 25% é 0.25, etc. Apenas uma maneira diferente de representar a mesma coisa.
Para o time com probabilidade de vencer de 50%, o odd será então:
$ \text{odd} = \frac{1}{0.5} = 2.0 $
Para os casos de empate e vitória do visitante, demos uma probabilidade de 25% para cada.
$ \text{odd} = \frac{1}{0.25} = 4.0$
Note que a soma das probabilidades dos três casos tem que ser 1.0, ou 100%:
$ 0.5 + 0.25 + 0.25 = 1.0 $
De volta ao exemplo real: como a casa de apostas faz dinheiro
Nós vimos acima uma oferta real de aposta de uma casa de aposta online. A oferta era:
Mandante: 1.909
X: 3.25
Visitante: 4.20
Como sabemos como transformar os odds em probabilidade, podemos aprender algo sobre qual a probabilidade que a casa de apostas definiu para cada resultado.
Para a vitória do mandante, a casa de apostas estima a seguinte probabilidade:
$ \text{probabilidade} = \frac{1}{1.909} = 0.524 = 52.4\% $
Para o empate, a casa de apostas estima:
$ \text{probabilidade} = \frac{1}{3.25} = 0.308 = 30.8\% $
E para a vitória do visitante, a casa de apostas estima:
$ \text{probabilidade} = \frac{1}{4.20} = 0.238 = 23.8\% $
Note como funciona a relação inversa do odd e da probabilidade estimadada: um odd menor (pagamento menor pela aposta) acontece quando a probabilidade é maior. Faz sentido: eventos menos prováveis pagam mais.
Agora, leitor perspicaz, note como há algo de estranho na soma das probabilidades:
$ 0.524 + 0.308 + 0.238 = 1.07 = 107\% $
Como a soma das probabilidades pode dar mais de 100%? Isso não deveria ser impossível?
Seria impossível apenas se a casa de apostas não tivesse fins lucrativos, como no nosso exemplo acima. O valor que a casa de apostas dá para o odd não é apenas o inverso da probabilidade estimada: o número é mexido para incluir uma comissão, e que no caso de apostas esportivas costumamos chamar de vigorish ou vig.
O efeito de fazer as probabilidades somarem um número maior do que 100% diminui o valor que tem que ser pago pela casa de apostas aos ganhadores. Isso porque, pela relação inversa, quando a probabilidade aumenta, o odd diminui, e o odd é proporcional ao que vai ser pago ao jogador em caso de vitória.
Como vencer a casa de apostas?
Recuperando a idéia acima, uma partida de futebol é um processo aleatório: você não sabe quem vai ganhar a partida. Alguns resultados são mais prováveis do que os outros, claro, mas quem apostou todo seu dinheiro em uma vitória clara da Argentina sobre a Arábia Saudita na Copa do Mundo perdeu todo seu dinheiro.
A alternativa correta para tentar vencer a casa de apostas é fazer várias pequenas apostas, apostando apenas no caso em que as probabilidades expostas via os odds que são oferecidos estiverem “erradas”: você tem que ter uma estimativa melhor do que da casa de apostas.
Sim, as probabilidades das casas de aposta são fantasticamente boas. Nós não conseguimos nunca saber qual a probabilidade real de vitória de um time em uma partida (teríamos que entrar no metaverso e rodar centenas de partidas em paralelo), mas podemos acompanhar os resultados de muitos jogos ao redor de anos e as estimativas feitas pelas casas de apostas – e ela são extraordinariamente boas. Se quiser uma boa estimativa da probabilidade real de resultados de um jogo, olhe para os resultados das casas de apostas mais competitivas: aqueles números serão muito próximos da realidade.
Não só isso, como também há o vig, a comissão que recebem. No caso que olhamos acima, a margem é de 7%. Isso quer dizer que, além de ser melhor do que a casa de apostas em estimar os resultados (o que é muito difícil), é também necessário fazer isso de maneira tão consistente e clara que consiga vencer os cerca de 7% de margem que são cobrados em cada aposta.
Isso é extremamente difícil, a ponto de que quem tem essas habilidades conseguirá fazer muito mais dinheiro simplesmente trabalhando como analista de dados ou para o mercado financeiro, onde esse tipo de análise pode ser usado em coisas que geram dinheiro de maneira mais confiável.
E isso, presumindo honestidade. As casas de apostas que existem no Brasil são todas empresas sediadas em países exóticos e com poucas proteções ao consumidor. Quando um apostador informado e capaz de vencer a casa de apostas aparecer, ela pode simplesmente:
- fechar a conta do apostador, por falta de interesse comercial. (e isso nem é ilegal), ou
- se recusar a pagar os prêmios do jogador, e se proteger no fato de que a empresa fica nas Filipinas e poucas pessoas vão se dar ao trabalho de entrar na justiça desse país
- confiscar o dinheiro do apostador alegando que alguma forma não-detectada de trapaça está envolvida.
Note que os meios ilegais nem são necessários para que a casa de apostas seja lucrativa: o vig em si já torna o negócio altamente lucrativo. Mas apostadores em mercados não-regulados como o Brasil ainda estão expostos ao risco de contra-parte adicional.
O futuro
Em posts futuros eu vou abordar vários aspectos de apostas esportivas: como um apostador pode tentar modelar as probabilidades, como ele deve escolher entre entrar em uma aposta ou não, como gerenciar o tamanho das apostas. E também do lado das casas de apostas, o que eles fazem para maximizar o dinheiro que recebem: o vig já tornaria esse negócio espetacular, mas casas de apostas são especialistas em aumentar seus lucros oferecendo apostas ruins como se fossem vantagem para o jogador na forma de ofertas exóticas, apostas casadas que não valem a pena, e vários apelos emocionais a apostas que não fazem sentido. Se tivermos energia vamos também olhar os oportunistas que vendem palpites em grupos de Telegram e como eles fazem para convencer apostadores a continuar pagando suas mensalidades, ao mesmo tempo que os usam para manipular mercados em seu favor.
Até lá, continuem não apostando!
Leia a parte 2 desse artigo
Fediverso: @zorked@mathstodon.xyz