zrk

Atenção: apostas esportivas são feitas para você perder. O retorno esperado de apostas esportivas é perder dinheiro. Sites de apostas esportivas não são confiáveis: mesmo se você ganhar, pode perder o prêmio por fraude. O fato de eu escrever sobre o assunto não quer dizer que eu sou a favor. Não gaste dinheiro com apostas esportivas. Jamais ache que apostas esportivas são uma fonte de renda. Se você ler a série que vou escrever vai saber detalhes de como isso funciona, mas quero botar a conclusão já aqui em cima. Simplesmente. Não. Aposte.

Essa é a parte 2. A parte 1 desse artigo está aqui.

O cassino sempre vence – eventualmente

Dos jogos de cassino, o mais simples de compreender como funciona é a roleta.

Nesse jogo, apostadores podem escolher vários tipos de apostas: números entre 1 e 36, números pares ou ímpares, números pretos ou vermelhos e algumas outras combinações. Mesmo que haja várias pessoas jogando simultaneamente, todos apostam contra a casa. Vamos considerar inicialmente que a roleta contém apenas os números de 1 a 36.

Digamos que algum apostador aposte nos números pares. Um funcionário do cassino gira a roleta. Caso a bolinha termine em um número par (2, 4, 6...), o apostador recebe o dobro da sua aposta. Caso caia em um número ímpar, perde a aposta. Metade dos números é par, portanto a probabilidade de o sorteio retornar um número par é 50%, ou 0.5. Os odds oferecidos pela roleta são justos:

$ \text{odd} = \frac{1}{0.5} = 2.0 $

Ou seja, se o apostador apostar R$ 10, ele receberá, em reais:

$ 10 \times 2.0 = 20 $

Como o apostador teve que colocar R\$ 10 na mesa para jogar, o lucro que teve é de R\$ 10.

E se o apostador quiser apostar em um número específico? Por exemplo, o número 33. Há 36 números na roleta, o que significa que a probabilidade de cair um determinado número é uma em 36:

$ p = \frac{1}{36} \approx 0.028 = 2.8\%$

O cassino oferece, usando um termo das apostas esporitvas, o seguinte odd:

$ \text{odd} = \frac{1}{0.028} = 36.0 $

Não é coincidência que o odd é 36.0, realmente está relacionado ao fato de ser um em 36. Esse é o odd justo: o cassino retorna todo o dinheiro que recebe para os apostadores, sem lucrar com nada.

Um apostador que aposte R$ 10 em um número específico, se vencedor, receberá, em reais:

$ 10 \times 36.0 = 360 $

Faz sentido que o prêmio seja muito maior para o caso de número individual do que no caso de números pares: é muito mais difícil acertar um número individual do que qualquer número par.

Vamos montar um cassino

Vamos nos colocar do lado de um cassino agora. Digamos que começamos com um investimento de R$ 1.000 e que, pela nossa regra da casa e para simplificar o exemplo, só aceitamos apostas em números específicos.

Podemos ter, por exemplo, uma sequência assim

Valor da banca: R\$ 1010 Apostada 1 – jogador perde R\$ 10 Valor da banca: R\$ 1010 Apostada 2 – jogador perde R\$ 10 Valor da banca: R\$ 1020 Apostada 3 – jogador perde R\$ 10 Valor da banca: R\$ 1030

Por enquanto nosso cassino só lucrou. Mas daí chega um novo apostador, que ganha:

Apostada 4 – jogador ganha R\$ 10 x 35 = R\$ 350 Valor da banca: R$ 680

Esse foi um passo para trás, e agora o cassino está em prejuízo. Muitos outros apostadores chegarão. Alguns ganharão, outros perderão. Os apostadores terão sequências de sorte ou de azar.

A questão é, qual o valor esperado da nossa banca após muitos meses de partidas? Nosso cassino perderá ou ganhará dinheiro?

A resposta é bastante simples usando a intuição: em 35 dos 36 números apostados, o cassino ganha R\$10. E um número a cada 36, ele perde R\$ 350. O valor esperado, após infinitas apostas, é:

$ E(V) = 0$

Mas estamos falando de um processo aleatório. Embora, no infinito, isso seja verdade, jogada a jogada o cassino ficará às vezes no lucro e às vezes no prejuízo.

Vamos rodar uma simulação. O cassino começa com um investimento de R$ 100.000

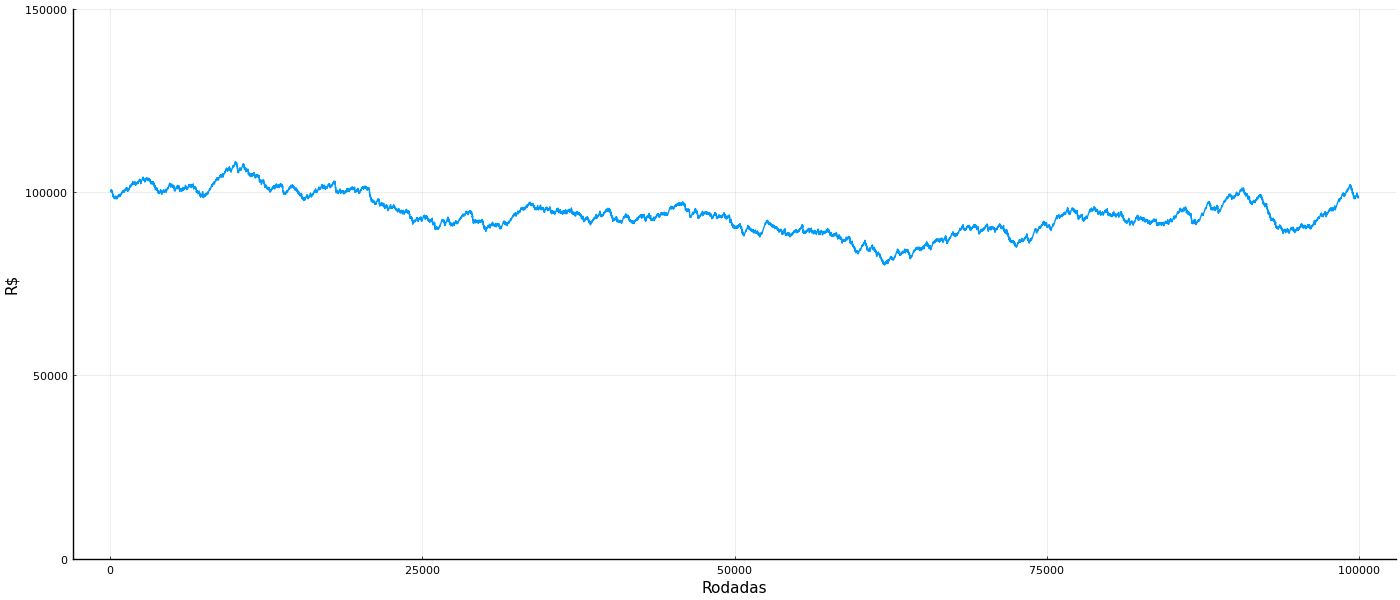
Esse gráfico mostra a simulação de cem mil rodadas com uma aposta cada. Note que o cassino começa com cem mil reais, e às vezes ele fica acima disso, às vezes abaixo, mas no geral tende a ter a mesma quantidade de dinheiro. Uma simulação assim é chamada de realização: é um caminho possível.

Podemos rodar a simulação várias vezes para verificar várias realizações possíveis:

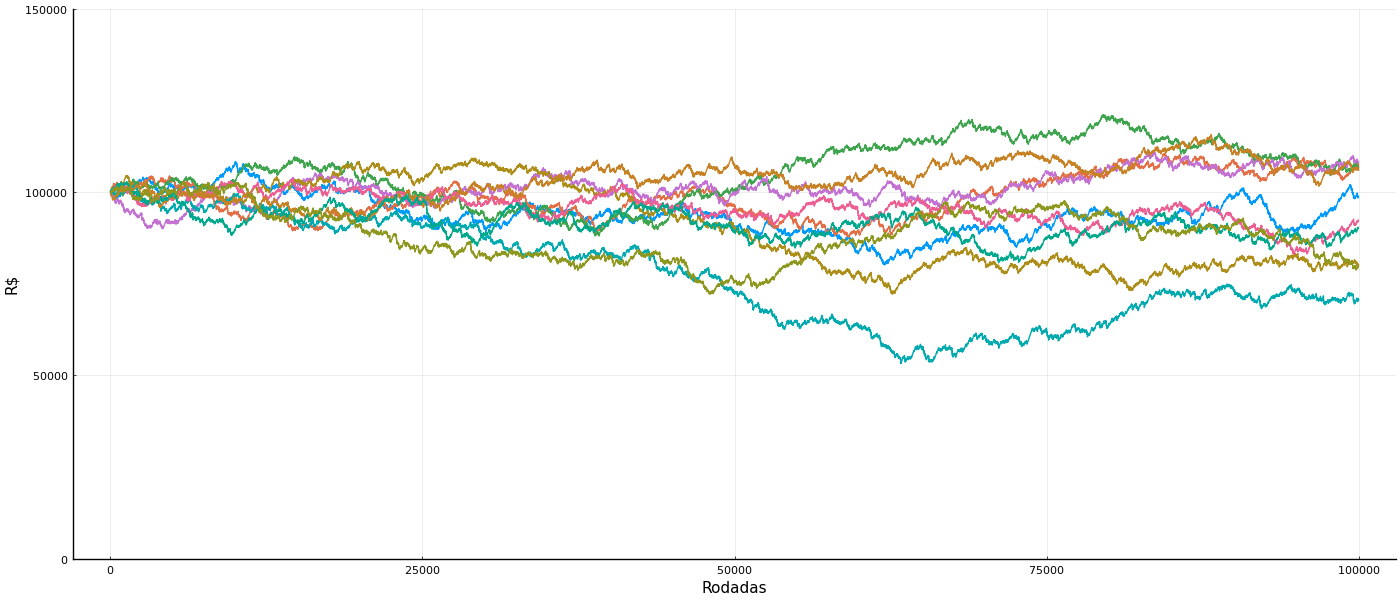
Note que algumas realizações divergem bastante. Uma delas chegou a ter 40% de prejuízo em um momento, antes de se recuperar. Outra chegou a ter cerca de vinte mil reais de lucro antes de retroceder. Na média, elas tendem a se manter sem lucro, mas as realizações podem variar bastante! Estruturalmente, não há nada que impeça um cassino como esse de ir à falência: perder todo seu dinheiro até não ter mais como pagar sua dívida com o apostador. É improvável, mas não é impossível.

Roubando a favor do cassino

Até agora definimos roleta como um jogo em que um número entre 1 e 36 é sorteado, mas a roleta de verdade também tem um número zero.

O número zero da roleta é especial: ele não é par, ele não é ímpar, e o apostador não pode apostar no zero. Quando a bolinha cai no zero, o cassino fica com todo o dinheiro apostado.

É isso que faz o cassino consistentemente ganhar dinheiro.

Com a nossa roleta honesta acima, o valor esperado de rodadas infinitas apostas era zero. Com a adição do número zero na roleta, apenas um número a mais, um número que tem \(\frac{1}{37} = 2.7\%\) de chance de acontecer, o valor esperado do lucro do nosso cassino é:

$ E(V) = \infty $

Sim, infinito. Não quer dizer que o cassino sempre estará no lucro, mas se a roleta for girada um número suficiente de vezes, o viés da adição do número zero vai fazer o cassino tender a ganhar dinheiro.

Simulamos isso e fizemos um gráfico de várias realizações possíveis disso após 100.000 apostas. Veja o resultado:

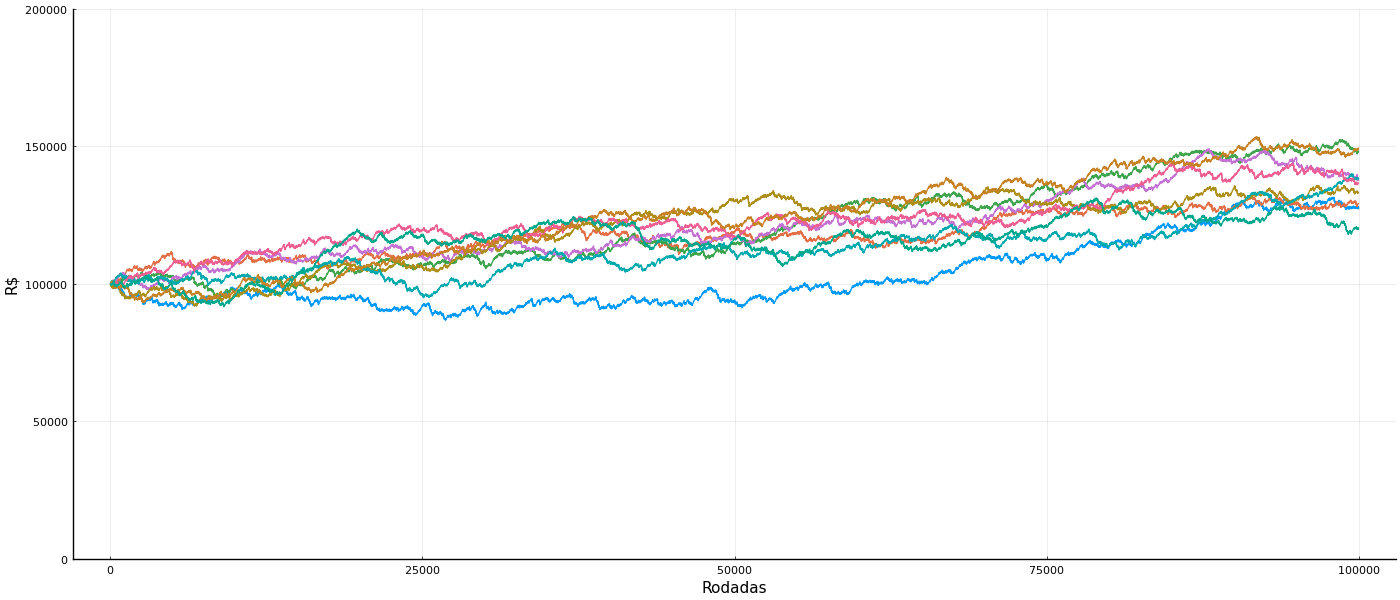
Note que a escala foi alterada desde o gráfico anterior. Ao invés de variar para cima e para baixo em torno do valor inicial, as realizações têm uma tendência de ir para cima. Na pior realização houve até um longo período de prejuízo, mas eventualmente a roleta passou a ser lucrativa para o cassino.

Uma simulação de 100.000 apostas parece muito? Em um cassino, a roleta gira em torno de 30 vezes por hora, e várias apostas podem ser realizadas ao mesmo tempo. Vamos supor conservadoramente que uma mesa recebe apenas três apostas por giro, e que o cassino abre por 4 horas por dia cerca de 300 dias por ano:

$ 30 \times 3 \times 6 = 108000$

Portanto o que simulamos é pouco menos que um ano de atividade de uma roleta. Considere que o cassino pode ter várias roletas, e que a aposta pode ser bem maior do que os R$ 10 que usamos aqui. No Cassino de Monte Carlo, em Mônaco, a menor aposta é de € 5, cerca de R\$ 26 quando escrevo isso.

Vamos calcular qual o valor esperado de exatamente 100.000 apostas de R\$ 26 em números individuais em uma roleta com números de zero a 36, como a usada no Cassino de Monte Carlo. Podemos pensar que em \(\frac{36}{37}\) das vezes o cassino vai lucrar R\$ 26, e em \(\frac{1}{37}\) vai perder R\$ 884, tudo isso multiplicado por 100.000 apostas:

$ 100000 \times (\frac{36}{37} \times 26 + \frac{1}{37} \times (-884)) \cong 140540$

Então em uma única roleta, o lucro anual sob premissas extremamente conservadoras é de R$ 140.450. Posso garantir que o apostador médio em Monte Carlo aposta consideravelmente mais do que 5 euros.

Um jogador pode vencer contra o cassino?

Um único jogador pode jogar uma partida e ganhar do cassino, recebendo um prêmio de 36 vezes sua aposta. Ele pode conseguir fazer isso duas, três, quatro vezes. Mas, se continuar jogando infinitas vezes, ele sempre vai perder. A única sorte que pode existir é parar enquanto está ganhando.

Mas nenhum jogador vai jogar infinitamente. Vamos simular 100.000 apostadores jogando o jogo acima de apostar R\$ 10 em um número específico, e vamos dizer que cada apostador fez 300 apostas em sua vida – cerca de 10 horas de jogo de roleta.

Disso tiramos um histograma, que mostra quantos jogadores ganharam quanto dinheiro.

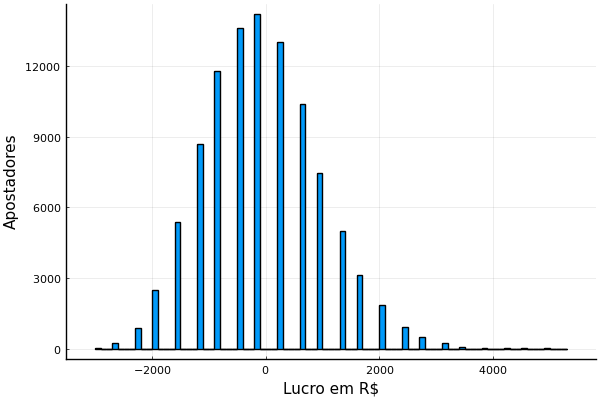
O valor das apostas é discreto, por isso o histograma tem buracos: por exemplo, é impossível terminar a sessão de apostas com lucro de R\$ 1 porque sempre apostamos, vencemos e perdemos em múltiplos de 10. Note que a maior quantidade de apostadores perdeu um pouco de dinheiro (a barra mais alta). Quantidades cada vez menores ganharam muito ou perderam muito.

Nesse caso, e é difícil ver isso no gráfico, o maior valor ganho foi R\$ 5.280, e o maior valor perdido for R\$ 3000 – isso quer dizer que pelo menos um dos apostadores simulados perdeu todas as 300 apostas que fez. 57,33% dos jogadores perdeu dinheiro.

E o que aconteceria se ao invés de parar em 300 jogos, os apostadores continuassem apostando até completar 3.000 jogos, dez vezes mais? Mais ou menos jogadores teriam lucro? O maior e o menor lucro mudariam de que forma?

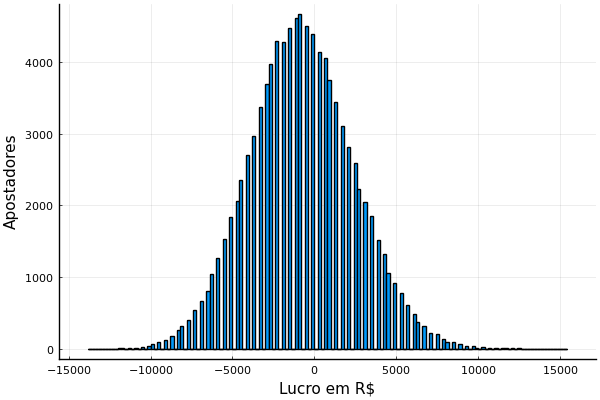
Note como a escala do gráfico muda: os valores mínimos e máximos são maiores, como esperado. A parte mais alta do gráfico se deslocou mais para a esquerda, mostrando que mais jogadores perderam dinheiro.

Nesse caso, o maior lucro foi R\$ 15.360, e o maior prejuízo foi de R\$ 13.800. Para um número de partidas dez vezes maior, o lucro máximo foi menos que três vezes maior. O maior prejuízo, porém, está mais do que quatro vezes maior. Nesse caso, 61,24% dos jogadores perdeu dinheiro.

É uma areia movediça. Quanto mais se joga, maior a probabilidade de perder. E não há estratégia que mude isso: o jogador só pode escolher o número em que aposta, mas em nada influencia o resultado: a roleta vai retornar um dos números, na mesma proporção, em uma ordem absolutamente imprevisível. Apostadores desinformados gostam de inventar estratégias, normalmente envolvendo aumentar as apostas depois de ganhar por estar “com sorte”. Nada disso funciona.

Uma quantidade considerável de jogadores vai ganhar dinheiro na roleta! E isso faz parte do apelo: é muito fácil conhecer alguém que ganhou dinheiro, e isso ajuda o marketing do cassino. Mas a maioria dos jogadores perde, e isso é suficiente para que o cassino lucre.

Algumas constatações:

1. O cassino não precisa trapaçear usando roletas viciadas que evitam os números apostados. Com o número zero na roleta, a tendência do cassino é ganhar dinheiro, e a do apostador, perder dinheiro.

2. Em espaços curtos de tempo, é possível para o apostador ganhar dinheiro. Mas, jogando por tempo o suficiente, o apostador tende a perder tudo.

3. Não há, no jogo de roleta, estratégia que permita ao apostador ganhar de forma consistente. O apostador não tem nenhum controle sobre se vai ganhar a próxima jogada.

4. Uma vantagem muito pequena para o cassino – apenas 2.7%! – permite ao cassino fazer muito dinheiro e ter uma vantagem muito grande sobre o apostador. Isso é um resultado pouco intuitivo, e a ele se soma o fato de que seqüências de jogadas sortudas podem fazer o jogador superestimar sua própria capacidade de ganhar.

O cassino sempre vence – eventualmente.

De volta às apostas esportivas

Na primeira parte desse post, nós vimos que uma aposta esportiva que encontramos na Internet tinha uma comissão escondida chamada vig. Fazendo contas que vamos desenvolver mais tarde, chegamos à conclusão de que o vig daquela oferta implica o que seria uma vantagem de 6.55% para a casa de apostas! Isso é muito mais do que a vantagem que o cassino tem na roleta. Nós vimos como uma pequena vantagem pode fazer uma diferença enorme na capacidade do apostador ganhar.

No caso da roleta, o número zero está visível, e é bem claro para os jogadores que ali está uma vantagem para o cassino – e ainda assim os apostadores estimam muito mal o impacto daquela vantagem. No caso da aposta esportiva, esse número está obscurecido.

Mas no caso da aposta esportiva, há um outro lado: números na roleta são todos iguais, mas o resultado do futebol parece mais previsível. Se houver um jogo entre a Argentina e Azerbaijão, parece muito previsível que a Argentina ganhe. Se perguntar para as pessoas quem vai ganhar o próximo jogo em um campeonato, o resultado mais esperado vai ser o correto uma quantidade grande de vezes. E é possível que pessoas que “entendem de futebol” sejam ainda melhores que os demais.

O jogo da roleta é um jogo de sorte pura, mas a aposta esportiva parece ter um componente influenciável – uma pessoa que entende de futebol não deveria acertar mais a aposta? Se você fosse apostar em quem ganharia uma partida de rugby entre os times irlandeses Connacht e Munster, talvez escolhesse aleatoriamente e tivesse pouca chance de estar certo, mas entre o Flamengo e o Paraná Club, tendo o conhecimento que temos, não é muito mais fácil prever quem vai vencer? Isso não torna a aposta esportiva um jogo em que a habilidade do apostador influencia o resultado, não do jogo, mas da aposta?

No próximo artigo veremos que a resposta é que sim – aposta esportiva não é um jogo puramente de sorte e, no entanto, isso pode não ser suficiente.

Fediverso: @zorked@mathstodon.xyz